Evaluates the goodness of fit of the return curve estimates
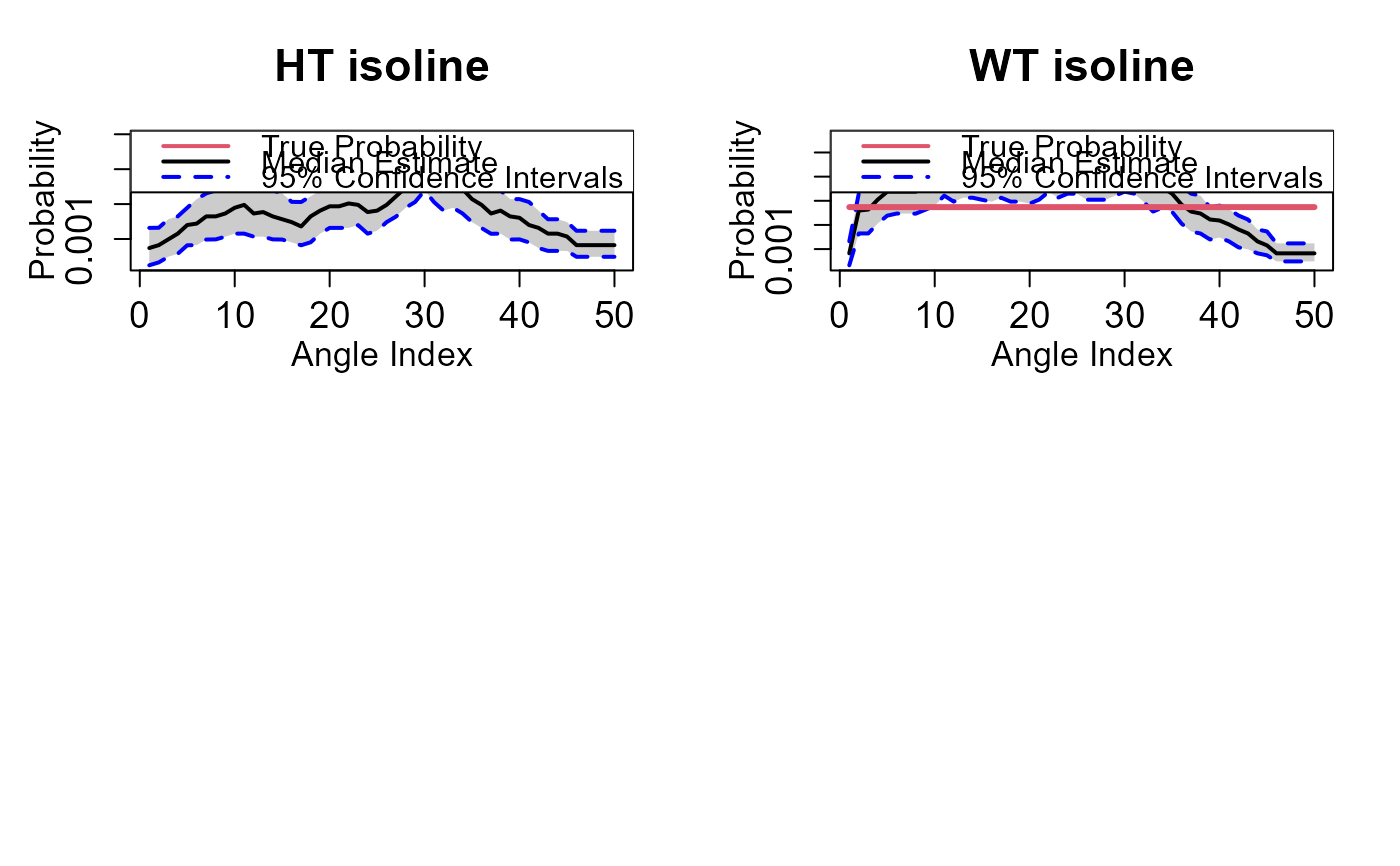
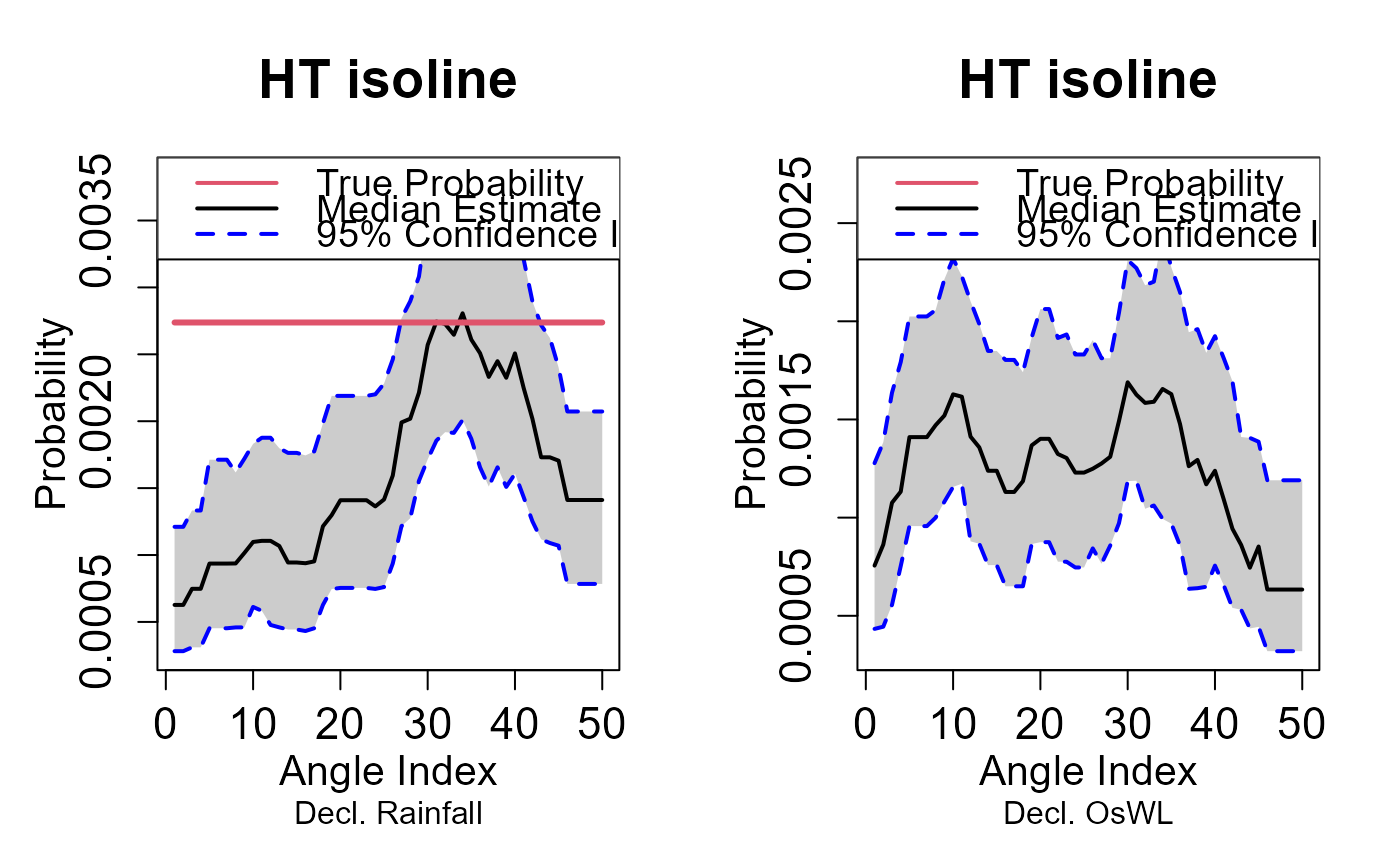
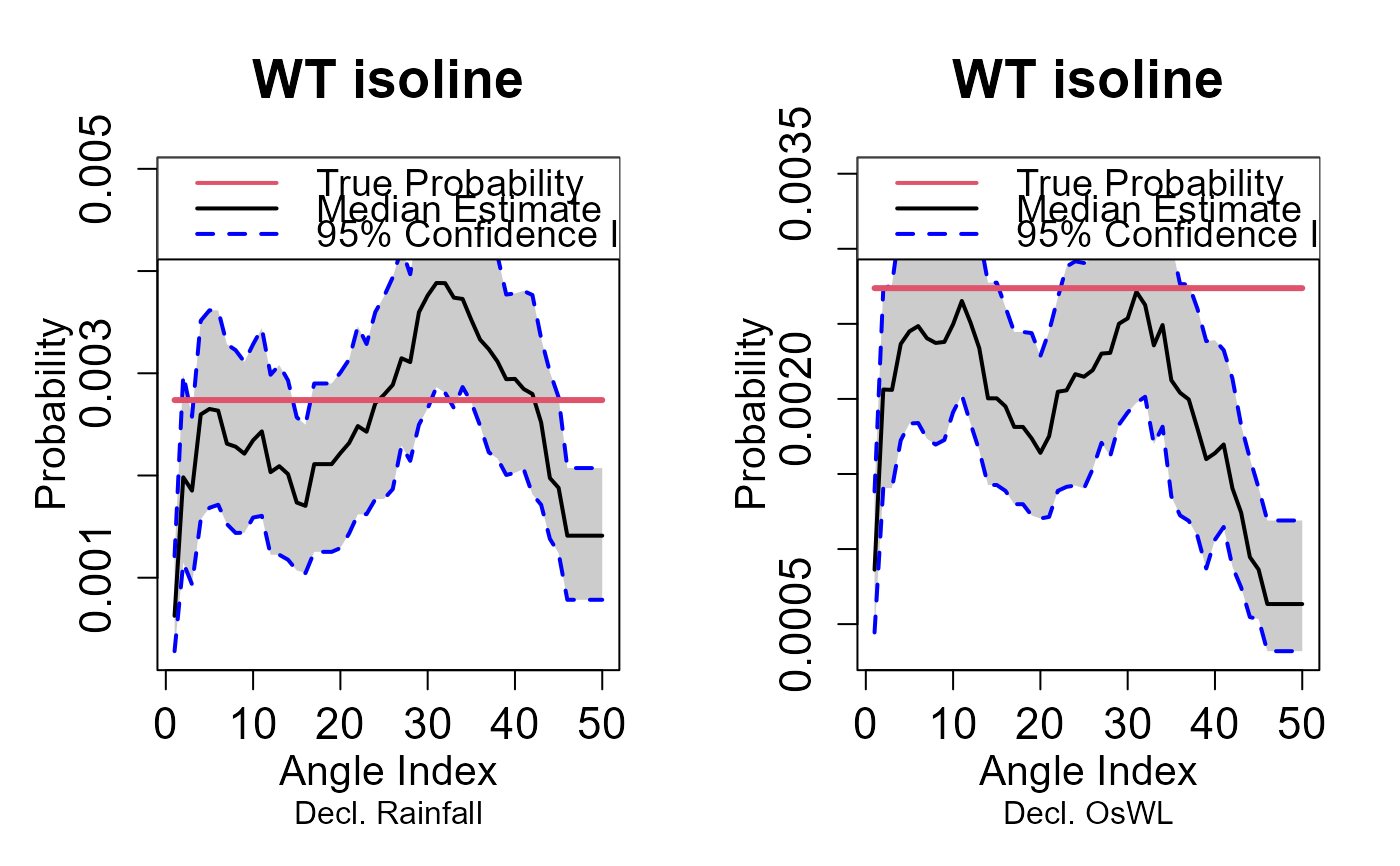
return_curve_diag.RdThe procedure calculates the empirical probability of observing data within the survival regions defined by a subset of points on the return curve. If the curve is a good fit, the empirical probabilities should closely match the probabilities associated with the return level curve. The procedure which is introduced in Murphy-Barltrop et al. (2023) uses bootstrap resampling of the original data set to obtain confidence intervals for the empirical estimates.
Usage
return_curve_diag(
data,
q,
rp,
mu,
n_sim,
n_grad,
n_boot,
boot_method,
boot_replace,
block_length,
boot_prop,
decl_method_x,
decl_method_y,
window_length_x,
window_length_y,
u_x = NA,
u_y = NA,
sep_crit_x = NA,
sep_crit_y = NA,
boot_method_all = "block",
boot_replace_all = NA,
block_length_all = 14,
boot_prop_all = 0.8,
alpha = 0.1,
x_lim_min = min(data[, 2], na.rm = TRUE),
x_lim_max = max(data[, 2], na.rm = TRUE) + 0.3 * diff(range(data[, 2], na.rm = TRUE)),
y_lim_min = min(data[, 3], na.rm = TRUE),
y_lim_max = max(data[, 3], na.rm = TRUE) + 0.3 * diff(range(data[, 2], na.rm = TRUE))
)Arguments
- data
Data frame of raw data detrended if necessary. First column should be of class
Date.- q
Numeric vector of length one specifying quantile level for fitting GPDs and the HT04 and WT13 models.
- rp
Numeric vector of length one specifying return period of interest.
- mu
Numeric vector of length one specifying the (average) occurrence frequency of events in Data. Default is 365.25, daily data.
- n_sim
Numeric vector of length one specifying the number of simulations for HT model. Default is
50.- n_grad
Numeric vector of length one specifying number of number of rays along which to compute points on the curve. Default is
50.- n_boot
Numeric vector of length one specifying number of bootstrap samples. Default is
100.- boot_method
Character vector of length one specifying the bootstrap method. Options are
"basic"(default),"block"or"monthly".- boot_replace
Logical vector of length one specifying whether simple bootstrapping is carried out with
TRUEor withoutFALSEreplacement. Only required ifboot_method = "basic". Default isNA.- block_length
Numeric vector of length one specifying block length. Only required if
boot_method = "block". Default isNA.- boot_prop
Numeric vector of length one specifying the minimum proportion of non-missing values of at least of the variables for a month to be included in the bootstrap. Only required if
boot_method = "monthly". Default is0.8.- decl_method_x
Character vector of length one specifying the declustering method to apply to the first variable. Options are the storm window approach
"window"(default) and the runs method"runs".- decl_method_y
Character vector of length one specifying the declustering method to apply to the second variable. Options are the storm window approach
"window"(default) and the runs method"runs".- window_length_x
Numeric vector of length one specifying the storm window length to apply during the declustering of the first variable if
decl_method_x = "window".- window_length_y
Numeric vector of length one specifying the storm window length to apply during the declustering of the second variable if
decl_method_y = "window".- u_x
Numeric vector of length one specifying the threshold to adopt in the declustering of the first variable if
decl_method_x = "runs". Default isNA.- u_y
Numeric vector of length one specifying the threshold to adopt in the declustering of the second variable if
decl_method_y = "runs". Default isNA.- sep_crit_x
Numeric vector of length one specifying the separation criterion to apply during the declustering of the first variable if
decl_method_x = "runs". Default isNA.- sep_crit_y
Numeric vector of length one specifying the separation criterion to apply during the declustering of the second variable if
decl_method_y = "runs". Default isNA.- boot_method_all
Character vector of length one specifying the bootstrapping procedure to use when estimating the distribution of empirical (survival) probabilities from the original dataset (without any declustering). Options are
"basic"(default) and"block".- boot_replace_all
Character vector of length one specifying whether bootstrapping of original dataset (without any declustering) when estimating the distribution of empirical (survival) probabilities is carried out with
"TRUE"or without"FALSE"replacement. Only required ifboot_method_all = "basic". Default isNA.- block_length_all
Numeric vector of length one specifying block length. Only required if
boot_method_all = "block". Default is14.- boot_prop_all
Numeric vector of length one specifying the minimum proportion of non-missing values of at least one of the variables for a month to be included in the bootstrap. Only required if
boot_method_all = "monthly". Default is0.8.- alpha
Numeric vector of length one specifying the
100(1-alpha)%confidence interval. Default is0.1.- x_lim_min
Numeric vector of length one specifying x-axis minimum.
- x_lim_max
Numeric vector of length one specifying x-axis maximum.
- y_lim_min
Numeric vector of length one specifying y-axis minimum.
- y_lim_max
Numeric vector of length one specifying y-axis maximum.
Value
List comprising the angles "ang_ind" associated with the points on the curve for which the empirical probability estimates were calculated.
For the HT04 model: Median "med_x_ht04", lower "lb_x_ht04" and upper "ub_x_ht04" bounds associated with the probabilities calculated using the sample conditioned on the first variable.
Median "med_y_ht04", lower "lb_y_ht04" and upper "ub_y_ht04" bounds associated with the probabilities calculated using the sample conditioned on the second variable.
Median "med_ht04", lower "lb_ht04" and upper "ub_ht04" bounds associated with the original dataset (without any declustering).
For the WT13 model: Median "med_x_wt13", lower "lb_x_wt13" and upper "ub_x_wt13" bounds associated with the probabilities calculated using the sample conditioned on the first variable.
Median "med_y_wt13", lower "lb_y_wt13" and upper "ub_y_wt13" bounds associated with the probabilities calculated using the sample conditioned on the second variable.
Median "med_wt13", lower "lb_wt13" and upper "ub_wt13" bounds associated with the original dataset (without any declustering).
Details
The HT04 model is fit to two conditional samples. One sample comprises the declustered time series of the first variable paired with concurrent values of the other variable. The second sample is obtained in the same way but with the variables reversed. The empirical probabilities are calculated using these two conditional samples and the original dataset (without any declustering). The return period should be chosen to ensure there is sufficient data for estimating empirical probabilities, yet the curve is sufficiently 'extreme'. An example could be to consider the fit using the 1 year return period curve rather than the 100 year return period curve.
Examples
#Data starts on first day of 1948
head(S22.Detrend.df)
#> Date Rainfall OsWL Groundwater
#> 1 1948-01-01 0.00 NA NA
#> 2 1948-01-02 0.14 NA NA
#> 3 1948-01-03 0.00 NA NA
#> 4 1948-01-04 0.00 NA NA
#> 5 1948-01-05 0.00 NA NA
#> 6 1948-01-06 0.00 NA NA
#Dataframe ends on 1948-02-03
tail(S22.Detrend.df)
#> Date Rainfall OsWL Groundwater
#> 25962 2019-01-29 NA NA 2.69
#> 25963 2019-01-30 NA NA 2.68
#> 25964 2019-01-31 NA NA 2.65
#> 25965 2019-02-01 NA NA 2.64
#> 25966 2019-02-02 NA NA 2.62
#> 25967 2019-02-03 NA NA 2.60
#Adding dates to complete final month of combined records
final.month = data.frame(seq(as.Date("2019-02-04"),as.Date("2019-02-28"),by="day"),NA,NA,NA)
colnames(final.month) = c("Date","Rainfall","OsWL","Groundwater")
S22.Detrend.df.extended = rbind(S22.Detrend.df,final.month)
#Diagnostic plots for the return curves
return_curve_diag(data=S22.Detrend.df.extended[,1:3],
q=0.985,rp=1,mu=365.25,n_sim=100,
n_grad=50,n_boot=100,boot_method="monthly",
boot_replace=NA, block_length=NA, boot_prop=0.8,
decl_method_x="runs", decl_method_y="runs",
window_length_x=NA,window_length_y=NA,
u_x=0.95, u_y=0.95,
sep_crit_x=36, sep_crit_y=36,
alpha=0.1,
boot_method_all="block", boot_replace_all=NA,
block_length_all=14)
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: no non-missing arguments to min; returning Inf
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> Warning: NAs introduced by coercion to integer range
#> $ang_ind
#> [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
#> [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
#>
#> $med_x_ht04
#> 50% 50% 50% 50% 50% 50%
#> 0.0006270577 0.0006270577 0.0007475352 0.0007475352 0.0009361277 0.0009361277
#> 50% 50% 50% 50% 50% 50%
#> 0.0009361277 0.0009370132 0.0010153609 0.0010976949 0.0011059582 0.0011059582
#> 50% 50% 50% 50% 50% 50%
#> 0.0010679003 0.0009441391 0.0009441391 0.0009386041 0.0009525321 0.0012146979
#> 50% 50% 50% 50% 50% 50%
#> 0.0012981059 0.0014094868 0.0014094868 0.0014094868 0.0014094868 0.0013633386
#> 50% 50% 50% 50% 50% 50%
#> 0.0014150978 0.0015939048 0.0019909642 0.0020186051 0.0022135803 0.0025703064
#> 50% 50% 50% 50% 50% 50%
#> 0.0027449069 0.0027268159 0.0026461440 0.0028067090 0.0026098427 0.0025084275
#> 50% 50% 50% 50% 50% 50%
#> 0.0023311937 0.0024487318 0.0023247719 0.0025070280 0.0022474179 0.0020178517
#> 50% 50% 50% 50% 50% 50%
#> 0.0017302423 0.0017302423 0.0017051700 0.0014112114 0.0014112114 0.0014112114
#> 50% 50%
#> 0.0014112114 0.0014112114
#>
#> $lb_x_ht04
#> 5% 5% 5% 5% 5% 5%
#> 0.0002814245 0.0002814245 0.0003100150 0.0003100150 0.0004527039 0.0004527039
#> 5% 5% 5% 5% 5% 5%
#> 0.0004527039 0.0004589516 0.0004593442 0.0006120246 0.0005829544 0.0004774404
#> 5% 5% 5% 5% 5% 5%
#> 0.0004593442 0.0004433904 0.0004433904 0.0004320774 0.0004527039 0.0006270958
#> 5% 5% 5% 5% 5% 5%
#> 0.0007457042 0.0007542254 0.0007542254 0.0007542254 0.0007542254 0.0007466516
#> 5% 5% 5% 5% 5% 5%
#> 0.0007604458 0.0009365781 0.0012158942 0.0012746730 0.0015545337 0.0017144798
#> 5% 5% 5% 5% 5% 5%
#> 0.0018550375 0.0019181257 0.0019129161 0.0020094320 0.0018684688 0.0016550992
#> 5% 5% 5% 5% 5% 5%
#> 0.0015118075 0.0016555026 0.0015091720 0.0016071343 0.0014320641 0.0012517776
#> 5% 5% 5% 5% 5% 5%
#> 0.0011176033 0.0010899026 0.0010696418 0.0007840328 0.0007840328 0.0007840328
#> 5% 5%
#> 0.0007840328 0.0007840328
#>
#> $ub_x_ht04
#> 95% 95% 95% 95% 95% 95%
#> 0.001210786 0.001210786 0.001332766 0.001332766 0.001712291 0.001712291
#> 95% 95% 95% 95% 95% 95%
#> 0.001712291 0.001616890 0.001720041 0.001830608 0.001876496 0.001876496
#> 95% 95% 95% 95% 95% 95%
#> 0.001798362 0.001763319 0.001763319 0.001744616 0.001774289 0.001983189
#> 95% 95% 95% 95% 95% 95%
#> 0.002189299 0.002189411 0.002189411 0.002189411 0.002189411 0.002201032
#> 95% 95% 95% 95% 95% 95%
#> 0.002281413 0.002462034 0.002770269 0.002896318 0.003080994 0.003537814
#> 95% 95% 95% 95% 95% 95%
#> 0.003701937 0.003756947 0.003825881 0.003829480 0.003601383 0.003356351
#> 95% 95% 95% 95% 95% 95%
#> 0.003284726 0.003402024 0.003227023 0.003389584 0.003208652 0.002896225
#> 95% 95% 95% 95% 95% 95%
#> 0.002717587 0.002622427 0.002400811 0.002072664 0.002072664 0.002072664
#> 95% 95%
#> 0.002072664 0.002072664
#>
#> $med_y_ht04
#> 50% 50% 50% 50% 50% 50%
#> 0.0007555730 0.0008625836 0.0010759089 0.0011321934 0.0014100555 0.0014100555
#> 50% 50% 50% 50% 50% 50%
#> 0.0014100555 0.0014710247 0.0015198448 0.0016278692 0.0016159603 0.0014123627
#> 50% 50% 50% 50% 50% 50%
#> 0.0013578268 0.0012386579 0.0012386579 0.0011307415 0.0011307415 0.0011856645
#> 50% 50% 50% 50% 50% 50%
#> 0.0013678059 0.0014014111 0.0014014111 0.0013241126 0.0013035785 0.0012293313
#> 50% 50% 50% 50% 50% 50%
#> 0.0012293313 0.0012490014 0.0012757185 0.0013097983 0.0014915040 0.0016893845
#> 50% 50% 50% 50% 50% 50%
#> 0.0016261963 0.0015842857 0.0015901984 0.0016553005 0.0016289379 0.0014763265
#> 50% 50% 50% 50% 50% 50%
#> 0.0012617717 0.0012940856 0.0011695976 0.0012387391 0.0010938057 0.0009432984
#> 50% 50% 50% 50% 50% 50%
#> 0.0008610020 0.0007448792 0.0008529710 0.0006336801 0.0006336801 0.0006336801
#> 50% 50%
#> 0.0006336801 0.0006336801
#>
#> $lb_y_ht04
#> 5% 5% 5% 5% 5% 5%
#> 0.0004332827 0.0004444452 0.0005558464 0.0007534134 0.0009568469 0.0009568469
#> 5% 5% 5% 5% 5% 5%
#> 0.0009568469 0.0010000337 0.0010809214 0.0011565866 0.0011725343 0.0008792135
#> 5% 5% 5% 5% 5% 5%
#> 0.0008669322 0.0007581065 0.0007581065 0.0006501991 0.0006501991 0.0006503184
#> 5% 5% 5% 5% 5% 5%
#> 0.0008653374 0.0008749913 0.0008749913 0.0007757146 0.0007753043 0.0007461346
#> 5% 5% 5% 5% 5% 5%
#> 0.0007461346 0.0008432988 0.0007652325 0.0008575529 0.0009714054 0.0011858577
#> 5% 5% 5% 5% 5% 5%
#> 0.0011879948 0.0010452778 0.0010617452 0.0009935016 0.0009694455 0.0008578830
#> 5% 5% 5% 5% 5% 5%
#> 0.0006374625 0.0006405706 0.0006477034 0.0007556540 0.0006562857 0.0005403070
#> 5% 5% 5% 5% 5% 5%
#> 0.0005308968 0.0004357109 0.0004436054 0.0003198227 0.0003198227 0.0003198227
#> 5% 5%
#> 0.0003198227 0.0003198227
#>
#> $ub_y_ht04
#> 95% 95% 95% 95% 95% 95%
#> 0.001277459 0.001383914 0.001636312 0.001792307 0.002024607 0.002024607
#> 95% 95% 95% 95% 95% 95%
#> 0.002024607 0.002057803 0.002214168 0.002319419 0.002229612 0.002101656
#> 95% 95% 95% 95% 95% 95%
#> 0.001985892 0.001848989 0.001848989 0.001803254 0.001803254 0.001740537
#> 95% 95% 95% 95% 95% 95%
#> 0.001916895 0.002062337 0.002062337 0.001914896 0.001932902 0.001830927
#> 95% 95% 95% 95% 95% 95%
#> 0.001830927 0.001904119 0.001811840 0.001811840 0.002042813 0.002311831
#> 95% 95% 95% 95% 95% 95%
#> 0.002270714 0.002183500 0.002201999 0.002438435 0.002274689 0.002147856
#> 95% 95% 95% 95% 95% 95%
#> 0.001944343 0.001959898 0.001839454 0.001924271 0.001812558 0.001694961
#> 95% 95% 95% 95% 95% 95%
#> 0.001410580 0.001406196 0.001386518 0.001190225 0.001190225 0.001190225
#> 95% 95%
#> 0.001190225 0.001190225
#>
#> $med_x_wt13
#> 50% 50% 50% 50% 50% 50%
#> 0.0006270577 0.0019821929 0.0018518752 0.0025970704 0.0026509028 0.0026340437
#> 50% 50% 50% 50% 50% 50%
#> 0.0023111460 0.0022817222 0.0022132564 0.0023445129 0.0024315286 0.0020325347
#> 50% 50% 50% 50% 50% 50%
#> 0.0020912175 0.0020135357 0.0017353586 0.0017029613 0.0021111633 0.0021111633
#> 50% 50% 50% 50% 50% 50%
#> 0.0021111633 0.0022190522 0.0023174423 0.0024837510 0.0024282415 0.0027061609
#> 50% 50% 50% 50% 50% 50%
#> 0.0027905962 0.0028864917 0.0031468948 0.0031094799 0.0035974371 0.0037610751
#> 50% 50% 50% 50% 50% 50%
#> 0.0038833261 0.0038816903 0.0037396406 0.0037271202 0.0035222055 0.0033298386
#> 50% 50% 50% 50% 50% 50%
#> 0.0032358495 0.0031145171 0.0029418807 0.0029450524 0.0028461531 0.0027974544
#> 50% 50% 50% 50% 50% 50%
#> 0.0025180447 0.0019752342 0.0018791172 0.0014112114 0.0014112114 0.0014112114
#> 50% 50%
#> 0.0014112114 0.0014112114
#>
#> $lb_x_wt13
#> 5% 5% 5% 5% 5% 5%
#> 0.0002814245 0.0011485402 0.0009354626 0.0015702816 0.0016839539 0.0017135907
#> 5% 5% 5% 5% 5% 5%
#> 0.0015245146 0.0014379730 0.0014399064 0.0015885745 0.0016054391 0.0012244066
#> 5% 5% 5% 5% 5% 5%
#> 0.0012244066 0.0011757653 0.0010716473 0.0010451522 0.0012530489 0.0012530489
#> 5% 5% 5% 5% 5% 5%
#> 0.0012530489 0.0012897679 0.0014327907 0.0016196673 0.0016217123 0.0017676346
#> 5% 5% 5% 5% 5% 5%
#> 0.0017705776 0.0018667469 0.0022931926 0.0021432945 0.0024975416 0.0026554949
#> 5% 5% 5% 5% 5% 5%
#> 0.0028645850 0.0028083249 0.0026602801 0.0028652714 0.0027160282 0.0024882946
#> 5% 5% 5% 5% 5% 5%
#> 0.0022267133 0.0021652537 0.0020048898 0.0020266175 0.0020622267 0.0018163000
#> 5% 5% 5% 5% 5% 5%
#> 0.0017135907 0.0013805884 0.0012400986 0.0007840328 0.0007840328 0.0007840328
#> 5% 5%
#> 0.0007840328 0.0007840328
#>
#> $ub_x_wt13
#> 95% 95% 95% 95% 95% 95%
#> 0.001210786 0.002988800 0.002575131 0.003514267 0.003615895 0.003615895
#> 95% 95% 95% 95% 95% 95%
#> 0.003284102 0.003225859 0.003111247 0.003283792 0.003440354 0.002985613
#> 95% 95% 95% 95% 95% 95%
#> 0.003080945 0.002930356 0.002569163 0.002496785 0.002900084 0.002900084
#> 95% 95% 95% 95% 95% 95%
#> 0.002900084 0.003006780 0.003135721 0.003460989 0.003286183 0.003598807
#> 95% 95% 95% 95% 95% 95%
#> 0.003752757 0.003939519 0.004221851 0.003968758 0.004496220 0.004712894
#> 95% 95% 95% 95% 95% 95%
#> 0.004923328 0.004925696 0.004715396 0.004923147 0.004670914 0.004242048
#> 95% 95% 95% 95% 95% 95%
#> 0.004211536 0.004150323 0.003770237 0.003781216 0.003805123 0.003765857
#> 95% 95% 95% 95% 95% 95%
#> 0.003340089 0.003012960 0.002764974 0.002072664 0.002072664 0.002072664
#> 95% 95%
#> 0.002072664 0.002072664
#>
#> $med_y_wt13
#> 50% 50% 50% 50% 50% 50%
#> 0.0008625836 0.0020626465 0.0020601799 0.0023658359 0.0024498822 0.0024851872
#> 50% 50% 50% 50% 50% 50%
#> 0.0024044664 0.0023727556 0.0023796649 0.0024974348 0.0026525307 0.0025076334
#> 50% 50% 50% 50% 50% 50%
#> 0.0023377324 0.0020039028 0.0020039028 0.0019499513 0.0018134906 0.0018134906
#> 50% 50% 50% 50% 50% 50%
#> 0.0017367777 0.0016407086 0.0017517306 0.0020479660 0.0020572800 0.0021648664
#> 50% 50% 50% 50% 50% 50%
#> 0.0021478877 0.0021919365 0.0023019785 0.0023066797 0.0025008458 0.0025365436
#> 50% 50% 50% 50% 50% 50%
#> 0.0027140086 0.0026258527 0.0023565484 0.0024922839 0.0021247672 0.0020412601
#> 50% 50% 50% 50% 50% 50%
#> 0.0019964130 0.0018011343 0.0015988447 0.0016389302 0.0016966228 0.0014047227
#> 50% 50% 50% 50% 50% 50%
#> 0.0012422541 0.0009465268 0.0008634257 0.0006336801 0.0006336801 0.0006336801
#> 50% 50%
#> 0.0006336801 0.0006336801
#>
#> $lb_y_wt13
#> 5% 5% 5% 5% 5% 5%
#> 0.0004444452 0.0014057392 0.0014057392 0.0017238208 0.0018359920 0.0018394925
#> 5% 5% 5% 5% 5% 5%
#> 0.0017346981 0.0016958714 0.0017266851 0.0019116997 0.0020256943 0.0018355680
#> 5% 5% 5% 5% 5% 5%
#> 0.0016553572 0.0014266813 0.0014266813 0.0013875062 0.0012988562 0.0012988562
#> 5% 5% 5% 5% 5% 5%
#> 0.0012236052 0.0012034980 0.0012142797 0.0013879030 0.0014144832 0.0014233707
#> 5% 5% 5% 5% 5% 5%
#> 0.0014031411 0.0015340401 0.0017073984 0.0016191200 0.0018284589 0.0019097911
#> 5% 5% 5% 5% 5% 5%
#> 0.0019736790 0.0020146105 0.0016992944 0.0018149500 0.0013513193 0.0012241239
#> 5% 5% 5% 5% 5% 5%
#> 0.0011876391 0.0010850716 0.0008705944 0.0010622866 0.0011471053 0.0008830885
#> 5% 5% 5% 5% 5% 5%
#> 0.0007437063 0.0005468257 0.0005329667 0.0003198227 0.0003198227 0.0003198227
#> 5% 5%
#> 0.0003198227 0.0003198227
#>
#> $ub_y_wt13
#> 95% 95% 95% 95% 95% 95%
#> 0.001383914 0.002731280 0.002761669 0.003188829 0.003256029 0.003349023
#> 95% 95% 95% 95% 95% 95%
#> 0.003075014 0.003023073 0.003131514 0.003300029 0.003455175 0.003296479
#> 95% 95% 95% 95% 95% 95%
#> 0.003089884 0.002774391 0.002774391 0.002610974 0.002446171 0.002446171
#> 95% 95% 95% 95% 95% 95%
#> 0.002438435 0.002285769 0.002450840 0.002674853 0.002881846 0.002916807
#> 95% 95% 95% 95% 95% 95%
#> 0.002905336 0.002935851 0.003183611 0.003081670 0.003300176 0.003300190
#> 95% 95% 95% 95% 95% 95%
#> 0.003481980 0.003433167 0.003116260 0.003325047 0.003037358 0.002765197
#> 95% 95% 95% 95% 95% 95%
#> 0.002762799 0.002599221 0.002385157 0.002391292 0.002325056 0.002135756
#> 95% 95% 95% 95% 95% 95%
#> 0.001824001 0.001603666 0.001407134 0.001190225 0.001190225 0.001190225
#> 95% 95%
#> 0.001190225 0.001190225
#>
#> $med_ht04
#> 50% 50% 50% 50% 50% 50%
#> 0.0007414731 0.0008238590 0.0009886307 0.0011534025 0.0014005602 0.0014417532
#> 50% 50% 50% 50% 50% 50%
#> 0.0016477179 0.0016477179 0.0017301038 0.0018948756 0.0019772615 0.0017301038
#> 50% 50% 50% 50% 50% 50%
#> 0.0017712968 0.0016477179 0.0015653320 0.0014829461 0.0013593673 0.0016477179
#> 50% 50% 50% 50% 50% 50%
#> 0.0018124897 0.0019360685 0.0019360685 0.0020184544 0.0019772615 0.0017712968
#> 50% 50% 50% 50% 50% 50%
#> 0.0018124897 0.0019772615 0.0022244192 0.0024715769 0.0026363487 0.0028835063
#> 50% 50% 50% 50% 50% 50%
#> 0.0028011204 0.0025127698 0.0025539628 0.0024303839 0.0021420333 0.0019772615
#> 50% 50% 50% 50% 50% 50%
#> 0.0017301038 0.0018124897 0.0016477179 0.0016065250 0.0014005602 0.0013181743
#> 50% 50% 50% 50% 50% 50%
#> 0.0011534025 0.0011534025 0.0010710166 0.0008238590 0.0008238590 0.0008238590
#> 50% 50%
#> 0.0008238590 0.0008238590
#>
#> $lb_ht04
#> 5% 5% 5% 5% 5% 5%
#> 0.0002471577 0.0003295436 0.0004901961 0.0005767013 0.0008197397 0.0008238590
#> 5% 5% 5% 5% 5% 5%
#> 0.0009845115 0.0009886307 0.0010668973 0.0011534025 0.0011534025 0.0010668973
#> 5% 5% 5% 5% 5% 5%
#> 0.0010668973 0.0009886307 0.0009845115 0.0009021256 0.0008197397 0.0009062449
#> 5% 5% 5% 5% 5% 5%
#> 0.0011534025 0.0013181743 0.0013181743 0.0013181743 0.0013964409 0.0011534025
#> 5% 5% 5% 5% 5% 5%
#> 0.0012357884 0.0014829461 0.0016435986 0.0018948756 0.0020596474 0.0023891910
#> 5% 5% 5% 5% 5% 5%
#> 0.0020555281 0.0018124897 0.0018948756 0.0017301038 0.0014829461 0.0013140550
#> 5% 5% 5% 5% 5% 5%
#> 0.0011492832 0.0011534025 0.0009845115 0.0009886307 0.0009021256 0.0007414731
#> 5% 5% 5% 5% 5% 5%
#> 0.0006590872 0.0006590872 0.0006590872 0.0004901961 0.0004901961 0.0004901961
#> 5% 5%
#> 0.0004901961 0.0004901961
#>
#> $ub_ht04
#> 95% 95% 95% 95% 95% 95%
#> 0.001318174 0.001322294 0.001565332 0.001647718 0.001894876 0.002142033
#> 95% 95% 95% 95% 95% 95%
#> 0.002306805 0.002389191 0.002471577 0.002558082 0.002558082 0.002393310
#> 95% 95% 95% 95% 95% 95%
#> 0.002479815 0.002393310 0.002306805 0.002063767 0.002059647 0.002224419
#> 95% 95% 95% 95% 95% 95%
#> 0.002393310 0.002553963 0.002553963 0.002640468 0.002801120 0.002475696
#> 95% 95% 95% 95% 95% 95%
#> 0.002471577 0.002805240 0.003134783 0.003386060 0.003546713 0.003954523
#> 95% 95% 95% 95% 95% 95%
#> 0.003624979 0.003377822 0.003295436 0.003217169 0.002801120 0.002558082
#> 95% 95% 95% 95% 95% 95%
#> 0.002389191 0.002393310 0.002142033 0.002142033 0.002059647 0.001812490
#> 95% 95% 95% 95% 95% 95%
#> 0.001565332 0.001565332 0.001487065 0.001235788 0.001235788 0.001235788
#> 95% 95%
#> 0.001235788 0.001235788
#>
#> $med_wt13
#> 50% 50% 50% 50% 50% 50%
#> 0.000823859 0.002595156 0.002636349 0.003048278 0.003377822 0.003377822
#> 50% 50% 50% 50% 50% 50%
#> 0.003377822 0.003377822 0.003542594 0.003789751 0.004284067 0.004119295
#> 50% 50% 50% 50% 50% 50%
#> 0.004078102 0.004119295 0.003954523 0.003954523 0.004036909 0.003789751
#> 50% 50% 50% 50% 50% 50%
#> 0.003789751 0.003789751 0.003872137 0.004242874 0.004036909 0.003954523
#> 50% 50% 50% 50% 50% 50%
#> 0.004036909 0.003624979 0.003789751 0.003748558 0.003954523 0.004160488
#> 50% 50% 50% 50% 50% 50%
#> 0.004119295 0.003954523 0.003419015 0.003542594 0.003295436 0.002842313
#> 50% 50% 50% 50% 50% 50%
#> 0.002553963 0.002471577 0.002224419 0.002183226 0.002018454 0.001812490
#> 50% 50% 50% 50% 50% 50%
#> 0.001647718 0.001318174 0.001153403 0.000823859 0.000823859 0.000823859
#> 50% 50%
#> 0.000823859 0.000823859
#>
#> $lb_wt13
#> 5% 5% 5% 5% 5% 5%
#> 0.0003295436 0.0016477179 0.0016477179 0.0020596474 0.0023850717 0.0024715769
#> 5% 5% 5% 5% 5% 5%
#> 0.0024715769 0.0024674576 0.0026281101 0.0027970012 0.0032130499 0.0029658922
#> 5% 5% 5% 5% 5% 5%
#> 0.0031265447 0.0031265447 0.0030400395 0.0029617729 0.0031265447 0.0029658922
#> 5% 5% 5% 5% 5% 5%
#> 0.0029658922 0.0028835063 0.0030482781 0.0033695831 0.0031306640 0.0032954358
#> 5% 5% 5% 5% 5% 5%
#> 0.0032913165 0.0030441588 0.0030441588 0.0030441588 0.0032130499 0.0033778217
#> 5% 5% 5% 5% 5% 5%
#> 0.0032954358 0.0029617729 0.0025539628 0.0027187346 0.0025457242 0.0020555281
#> 5% 5% 5% 5% 5% 5%
#> 0.0017301038 0.0016435986 0.0013964409 0.0014788268 0.0013181743 0.0010710166
#> 5% 5% 5% 5% 5% 5%
#> 0.0009886307 0.0008238590 0.0007414731 0.0004901961 0.0004901961 0.0004901961
#> 5% 5%
#> 0.0004901961 0.0004901961
#>
#> $ub_wt13
#> 95% 95% 95% 95% 95% 95%
#> 0.001322294 0.003295436 0.003381941 0.003962762 0.004370572 0.004531224
#> 95% 95% 95% 95% 95% 95%
#> 0.004535344 0.004374691 0.004366452 0.004613610 0.005276817 0.005029659
#> 95% 95% 95% 95% 95% 95%
#> 0.005025540 0.005107926 0.004869006 0.004947273 0.005194431 0.004951392
#> 95% 95% 95% 95% 95% 95%
#> 0.004951392 0.004947273 0.004951392 0.005437469 0.005112045 0.005112045
#> 95% 95% 95% 95% 95% 95%
#> 0.005116164 0.004778382 0.004864887 0.004869006 0.005272697 0.005519855
#> 95% 95% 95% 95% 95% 95%
#> 0.005688746 0.005437469 0.004613610 0.004617729 0.004201681 0.003624979
#> 95% 95% 95% 95% 95% 95%
#> 0.003295436 0.003213050 0.002718735 0.002801120 0.002644587 0.002389191
#> 95% 95% 95% 95% 95% 95%
#> 0.002224419 0.001812490 0.001730104 0.001235788 0.001235788 0.001235788
#> 95% 95%
#> 0.001235788 0.001235788
#>
