Calculates joint and conditional return periods
Conditional_RP_2D_Equal.RdA large number of realizations are simulated from the copulas fit to the conditioned samples, in proportion with the sizes of the conditional samples. The realization are transformed to the original scale and the relevant probabilities estimated empirically. The conditional probabilities return period of the conditioning variable equals
Usage
Conditional_RP_2D_Equal(
Data,
Data_Con1,
Data_Con2,
u1,
u2,
Thres1 = NA,
Thres2 = NA,
Copula_Family1,
Copula_Family2,
Marginal_Dist1,
Marginal_Dist2,
Con1 = "Rainfall",
Con2 = "OsWL",
mu = 365.25,
Con_Var,
RP_Con,
RP_Non_Con,
Width = 0.1,
x_lab = "Rainfall (mm)",
y_lab = "O-sWL (mNGVD 29)",
x_lim_min = NA,
x_lim_max = NA,
y_lim_min = NA,
y_lim_max = NA,
DecP = 2,
N
)Arguments
- Data
Data frame of dimension
nx2containing two co-occurring time series of lengthn.- Data_Con1
Data frame containing the conditional sample (declustered excesses paired with concurrent values of other variable), conditioned on the variable in the first column.
- Data_Con2
Data frame containing the conditional sample (declustered excesses paired with concurrent values of other variable), conditioned on the variable in the second column. Can be obtained using the
Con_Sampling_2Dfunction.- u1
Numeric vector of length one specifying the (quantile) threshold above which the variable in the first column was sampled in
Data_Con1.- u2
Numeric vector of length one specifying the (quantile) threshold above which the variable in the second column was sampled in
Data_Con2.- Thres1
Numeric vector of length one specifying the threshold above which the variable in the first column was sampled in
Data_Con1. Only one ofu1andThres1should be supplied. Default isNA.- Thres2
Numeric vector of length one specifying the threshold above which the variable in the second column was sampled in
Data_Con2. Only one ofu2andThres2should be supplied. Default isNA.- Copula_Family1
Numeric vector of length one specifying the copula family used to model the
Data_Con1dataset.- Copula_Family2
Numeric vector of length one specifying the copula family used to model the
Data_Con2dataset. Best fitting of 40 copulas can be found using theCopula_Threshold_2Dfunction.- Marginal_Dist1
Character vector of length one specifying (non-extreme) distribution used to model the marginal distribution of the non-conditioned variable in
Data_Con1.- Marginal_Dist2
Character vector of length one specifying (non-extreme) distribution used to model the marginal distribution of the non-conditioned variable in
Data_Con2.- Con1
Character vector of length one specifying the name of variable in the first column of
Data.- Con2
Character vector of length one specifying the name of variable in the second column of
Data.- mu
Numeric vector of length one specifying the (average) occurrence frequency of events in
Data. Default is365.25, daily data.- Con_Var
Character vector of length one specifying the (column) name of the conditioning variable.
- RP_Con
Numeric vector of length one specifying the return period of the conditioning variable
Con_Var.- RP_Non_Con
Numeric vector of length one specifying the return period of the non-conditioning variable.
- Width
Numeric vector of length one specifying the distance above and below the
RP_Conevent ofCon_Varthe simulated events are used to estimate the conditional probability.- x_lab
Character vector specifying the x-axis label.
- y_lab
Character vector specifying the y-axis label.
- x_lim_min
Numeric vector of length one specifying x-axis minimum. Default is
NA.- x_lim_max
Numeric vector of length one specifying x-axis maximum. Default is
NA.- y_lim_min
Numeric vector of length one specifying y-axis minimum. Default is
NA.- y_lim_max
Numeric vector of length one specifying y-axis maximum. Default is
NA.- DecP
Numeric vector of length one specifying the number of decimal places to round the data in the conditional samples to in order to identify observations in both conditional samples. Default is
2.- N
Numeric vector of length one specifying the size of the sample from the fitted joint distributions used to estimate the density along an isoline. Samples are collected from the two joint distribution with proportions consistent with the total number of extreme events conditioned on each variable. Default is
10^6
Value
Console output:
Con_Var Name of the conditioning variable
RP_Var1 Return period of variable Con1 i.e., variable in second column of
DataRP_Var2 Return period of variable Con2 i.e., variable in third column of
DataVar1 Value of Con1 at the return period of interest
Var2 Value of Con2 at the return period of interest
RP_Full_Dependence Joint return period of the (Var1,Var2) event under full dependence
RP_Independence Joint return period of the (Var1,Var2) event under independence
RP_Copula Joint return period of the (Var1,Var2) event according to the two sided conditional sampling - copula theory approach
Prob Probability associated with
RP_CopulaN_Sub_Sample Number of realizations of the
Con_Varwithin +/- width of the value ofCon_Varwith return period.Non_Con_Var_X Values of the non-conditioned variable of the (conditional) Cummulative Distribution Function (CDF) i.e. x-axis of bottom left plot
Con_Prob
Con_ProbCDF of the non-conditioned variable given the return period ofCon_VarequalsRP_ConCon_Prob_Est Probability the non-conditioned variable is less than or equal to
RP_Non_Congiven the return period ofCon_VarequalsRP_Con
Graphical output:
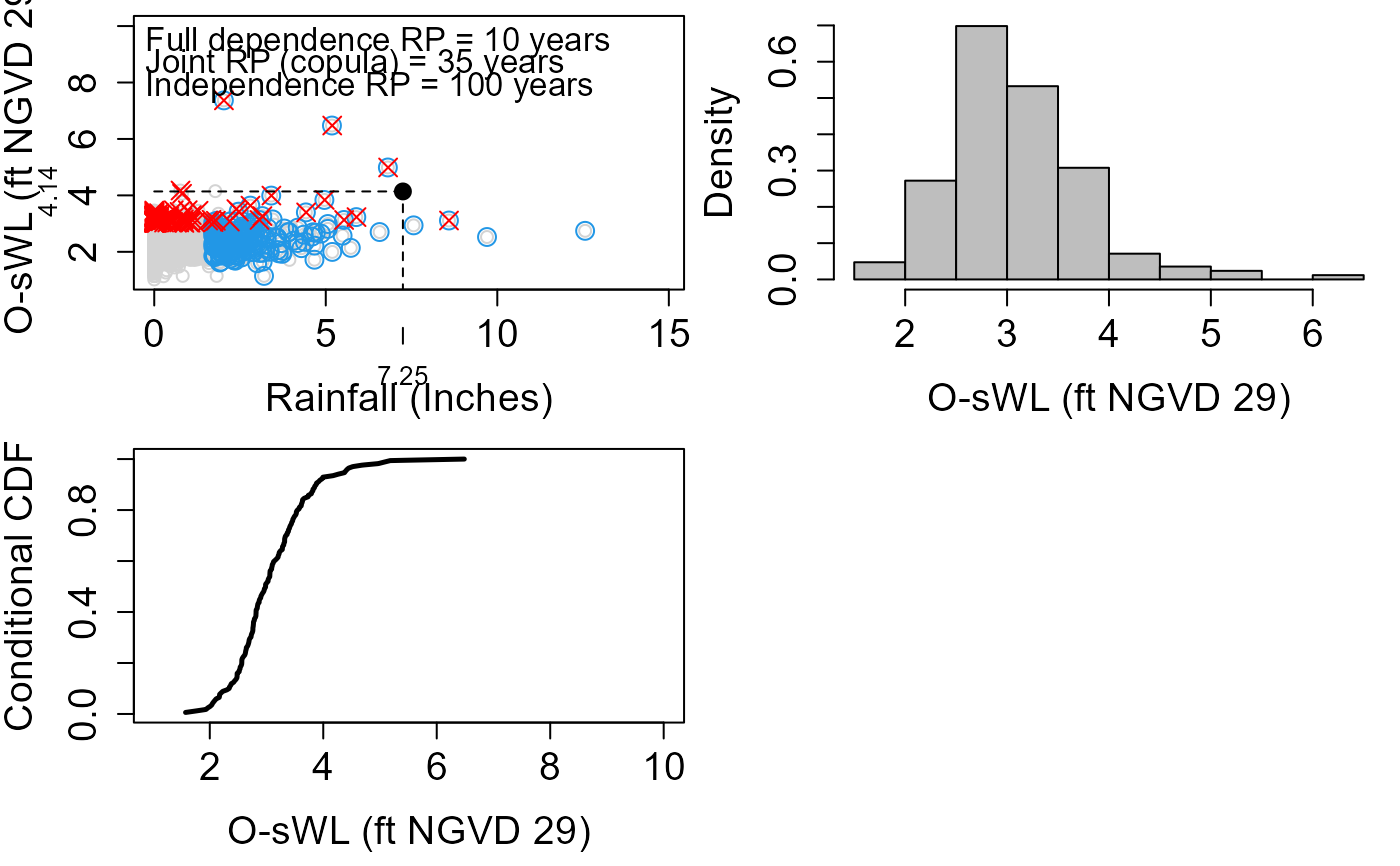
Top Left: Sample conditioned on rainfall (red crosses) and O-sWL (blue circles). Black dot is the event with a marginal return period of the conditioned variable
Var_Conand non-conditioned variable equal toRP_ConandRP_Non_Con, respectively. The joint return period of the event using the conditional sampling - copula theory approach and under the assumptions of full dependence and independence between the variables are printed.Top Right: Sample used to estimate the joint return period of the event of interest. Black dots denote the
N_Excesssized subset of the sample where the marginal return period of the conditioned variableVar_ConexceedsRP_Con(years). The subset is used to estimate the conditional probabilities in part two of the question.Bottom Left: Conditional Cumulative Distribution Function (CDF) of the non-conditioned variable given the marginal return period of the conditioned variable
Var_ConexceedsRP_Conyears i.e. the black dots in the top right plot.Bottom Right: Conditional return period of the non-conditioned variable given the conditioned variable
Var_Conhas a return period longer thanRP_Con.
Examples
#Under a 10yr rainfall event condition, what is the joint probability that a 10yr surge (O-sWL)
#event occurs simultaneously? What is the cumulative probability of events with the frequency
#equal to or less than a 10yr surge event?
#' #Conditional samples
con.sample.Rainfall<-Con_Sampling_2D(Data_Detrend=S22.Detrend.df[,-c(1,4)],
Data_Declust=S22.Detrend.Declustered.df[,-c(1,4)],
Con_Variable="Rainfall",u=0.98)
con.sample.OsWL<-Con_Sampling_2D(Data_Detrend=S22.Detrend.df[,-c(1,4)],
Data_Declust=S22.Detrend.Declustered.df[,-c(1,4)],
Con_Variable="OsWL",u=0.98)
#Add some noise to rainfall to aid distribution fitting in Conditional_RP_2D function
con.sample.OsWL$Data$Rainfall<-con.sample.OsWL$Data$Rainfall+
runif(length(con.sample.OsWL$Data$Rainfall),0.001,0.01)
#Find the best fitting copula
cop.Rainfall <- Copula_Threshold_2D(Data_Detrend=S22.Detrend.df[,-c(1,4)],
Data_Declust=S22.Detrend.Declustered.df[,-c(1,4)],
u1=0.98, u2=NA, PLOT=FALSE)$Copula_Family_Var1
cop.OsWL<- Copula_Threshold_2D(Data_Detrend=S22.Detrend.df[,-c(1,4)],
Data_Declust=S22.Detrend.Declustered.df[,-c(1,4)],
u1=NA, u2=0.98, PLOT=FALSE)$Copula_Family_Var2
#Calculate conditional probabilities
Conditional_RP_2D_Equal(Data=S22.Detrend.df,
Data_Con1=con.sample.Rainfall$Data, Data_Con2=con.sample.OsWL$Data,
u1=0.98, u2=0.98,
Copula_Family1=cop.Rainfall,Copula_Family2=cop.OsWL,
Marginal_Dist1="Logis", Marginal_Dist2="Twe",
Con1 = "Rainfall", Con2 = "OsWL",
mu = 365.25,
Con_Var="Rainfall",
RP_Con=10, RP_Non_Con=10,
x_lab = "Rainfall (Inches)", y_lab = "O-sWL (ft NGVD 29)",
y_lim_max = 10,
N=10^5)
#> Warning: NaNs produced
#> Warning: NaNs produced
#> Warning: non-list contrasts argument ignored
#> 1.5 1.7 1.9 2.1 2.3 2.5
#> ......Done.
#> $Con_Var
#> [1] "Rainfall"
#>
#> $RP_Var1
#> [1] 10
#>
#> $RP_Var2
#> [1] 10
#>
#> $Var1
#> [1] 7.248577
#>
#> $Var2
#> [1] 4.139639
#>
#> $RP_Full_Dependence
#> [1] 10
#>
#> $RP_Independence
#> [1] 100
#>
#> $RP_Copula
#> [1] 35.22067
#>
#> $Prob
#> [1] 0.02839242
#>
#> $N_Sub_Sample
#> [1] 169
#>
#> $Non_Con_Var_X
#> [1] 1.57 1.58 1.59 1.60 1.61 1.62 1.63 1.64 1.65 1.66 1.67 1.68 1.69 1.70 1.71
#> [16] 1.72 1.73 1.74 1.75 1.76 1.77 1.78 1.79 1.80 1.81 1.82 1.83 1.84 1.85 1.86
#> [31] 1.87 1.88 1.89 1.90 1.91 1.92 1.93 1.94 1.95 1.96 1.97 1.98 1.99 2.00 2.01
#> [46] 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 2.14 2.15 2.16
#> [61] 2.17 2.18 2.19 2.20 2.21 2.22 2.23 2.24 2.25 2.26 2.27 2.28 2.29 2.30 2.31
#> [76] 2.32 2.33 2.34 2.35 2.36 2.37 2.38 2.39 2.40 2.41 2.42 2.43 2.44 2.45 2.46
#> [91] 2.47 2.48 2.49 2.50 2.51 2.52 2.53 2.54 2.55 2.56 2.57 2.58 2.59 2.60 2.61
#> [106] 2.62 2.63 2.64 2.65 2.66 2.67 2.68 2.69 2.70 2.71 2.72 2.73 2.74 2.75 2.76
#> [121] 2.77 2.78 2.79 2.80 2.81 2.82 2.83 2.84 2.85 2.86 2.87 2.88 2.89 2.90 2.91
#> [136] 2.92 2.93 2.94 2.95 2.96 2.97 2.98 2.99 3.00 3.01 3.02 3.03 3.04 3.05 3.06
#> [151] 3.07 3.08 3.09 3.10 3.11 3.12 3.13 3.14 3.15 3.16 3.17 3.18 3.19 3.20 3.21
#> [166] 3.22 3.23 3.24 3.25 3.26 3.27 3.28 3.29 3.30 3.31 3.32 3.33 3.34 3.35 3.36
#> [181] 3.37 3.38 3.39 3.40 3.41 3.42 3.43 3.44 3.45 3.46 3.47 3.48 3.49 3.50 3.51
#> [196] 3.52 3.53 3.54 3.55 3.56 3.57 3.58 3.59 3.60 3.61 3.62 3.63 3.64 3.65 3.66
#> [211] 3.67 3.68 3.69 3.70 3.71 3.72 3.73 3.74 3.75 3.76 3.77 3.78 3.79 3.80 3.81
#> [226] 3.82 3.83 3.84 3.85 3.86 3.87 3.88 3.89 3.90 3.91 3.92 3.93 3.94 3.95 3.96
#> [241] 3.97 3.98 3.99 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 4.10 4.11
#> [256] 4.12 4.13 4.14 4.15 4.16 4.17 4.18 4.19 4.20 4.21 4.22 4.23 4.24 4.25 4.26
#> [271] 4.27 4.28 4.29 4.30 4.31 4.32 4.33 4.34 4.35 4.36 4.37 4.38 4.39 4.40 4.41
#> [286] 4.42 4.43 4.44 4.45 4.46 4.47 4.48 4.49 4.50 4.51 4.52 4.53 4.54 4.55 4.56
#> [301] 4.57 4.58 4.59 4.60 4.61 4.62 4.63 4.64 4.65 4.66 4.67 4.68 4.69 4.70 4.71
#> [316] 4.72 4.73 4.74 4.75 4.76 4.77 4.78 4.79 4.80 4.81 4.82 4.83 4.84 4.85 4.86
#> [331] 4.87 4.88 4.89 4.90 4.91 4.92 4.93 4.94 4.95 4.96 4.97 4.98 4.99 5.00 5.01
#> [346] 5.02 5.03 5.04 5.05 5.06 5.07 5.08 5.09 5.10 5.11 5.12 5.13 5.14 5.15 5.16
#> [361] 5.17 5.18 5.19 5.20 5.21 5.22 5.23 5.24 5.25 5.26 5.27 5.28 5.29 5.30 5.31
#> [376] 5.32 5.33 5.34 5.35 5.36 5.37 5.38 5.39 5.40 5.41 5.42 5.43 5.44 5.45 5.46
#> [391] 5.47 5.48 5.49 5.50 5.51 5.52 5.53 5.54 5.55 5.56 5.57 5.58 5.59 5.60 5.61
#> [406] 5.62 5.63 5.64 5.65 5.66 5.67 5.68 5.69 5.70 5.71 5.72 5.73 5.74 5.75 5.76
#> [421] 5.77 5.78 5.79 5.80 5.81 5.82 5.83 5.84 5.85 5.86 5.87 5.88 5.89 5.90 5.91
#> [436] 5.92 5.93 5.94 5.95 5.96 5.97 5.98 5.99 6.00 6.01 6.02 6.03 6.04 6.05 6.06
#> [451] 6.07 6.08 6.09 6.10 6.11 6.12 6.13 6.14 6.15 6.16 6.17 6.18 6.19 6.20 6.21
#> [466] 6.22 6.23 6.24 6.25 6.26 6.27 6.28 6.29 6.30 6.31 6.32 6.33 6.34 6.35 6.36
#> [481] 6.37 6.38 6.39 6.40 6.41 6.42 6.43 6.44 6.45 6.46 6.47 6.48 6.49
#>
#> $Con_Prob
#> [1] NA 0.006215124 0.006533218 0.006851312 0.007169406 0.007487500
#> [7] 0.007805594 0.008123688 0.008441782 0.008759876 0.009077970 0.009396064
#> [13] 0.009714158 0.010032251 0.010350345 0.010668439 0.010986533 0.011307058
#> [19] 0.011627690 0.011948321 0.012280211 0.012614264 0.012948318 0.013282371
#> [25] 0.013616424 0.013950477 0.014284530 0.014618583 0.014952637 0.015286690
#> [31] 0.015620743 0.015954796 0.016288849 0.016622903 0.016956956 0.017366987
#> [37] 0.017788256 0.018995220 0.020996200 0.022997181 0.024605579 0.026015707
#> [43] 0.027425836 0.028835964 0.030522906 0.032524199 0.034525493 0.037820697
#> [49] 0.042024269 0.044963923 0.047866659 0.050631488 0.053381530 0.056037616
#> [55] 0.058687296 0.060053146 0.061131858 0.062210571 0.063289283 0.064367995
#> [61] 0.069189559 0.078310111 0.080527343 0.082735257 0.084805896 0.086860187
#> [67] 0.088665476 0.089627222 0.090435260 0.091243299 0.092051337 0.092859376
#> [73] 0.093667414 0.094553373 0.095747893 0.097172179 0.098596465 0.100032216
#> [79] 0.106535534 0.109729530 0.113197105 0.118627945 0.120110681 0.121490339
#> [85] 0.122869997 0.124428531 0.127402666 0.130452978 0.132888323 0.135300528
#> [91] 0.138768658 0.145252971 0.160959118 0.162628352 0.164297586 0.170372271
#> [97] 0.175935082 0.185068440 0.188460594 0.194047774 0.215739008 0.220534545
#> [103] 0.223944101 0.226804609 0.229465836 0.233603447 0.242407919 0.252456423
#> [109] 0.261909469 0.264651868 0.268568356 0.274751171 0.283437646 0.293464345
#> [115] 0.297384829 0.299928079 0.307472599 0.315045551 0.319985954 0.332693659
#> [121] 0.354977390 0.365000385 0.374101421 0.377299209 0.382585005 0.408886727
#> [127] 0.412327333 0.421946209 0.432473700 0.435150722 0.437950475 0.450104116
#> [133] 0.453202457 0.459913821 0.465603719 0.469872246 0.473846205 0.476975555
#> [139] 0.480683291 0.487491775 0.493350990 0.496372852 0.510597008 0.513447928
#> [145] 0.516121418 0.518636443 0.527479548 0.532589573 0.536104378 0.551613728
#> [151] 0.563465661 0.565780354 0.568950206 0.582099492 0.588954660 0.593892973
#> [157] 0.598682724 0.600639673 0.602596622 0.604689658 0.606912053 0.609145897
#> [163] 0.611683364 0.614289829 0.622392555 0.626947186 0.635195683 0.638521389
#> [169] 0.640433738 0.642077026 0.643720314 0.651275564 0.658924219 0.661653284
#> [175] 0.670807519 0.686667804 0.695277101 0.699430427 0.701504319 0.703578210
#> [181] 0.711747858 0.714475294 0.723171325 0.726832262 0.733807184 0.738811663
#> [187] 0.742648551 0.747446922 0.753650676 0.757647429 0.765708845 0.769792304
#> [193] 0.774006477 0.777121380 0.779827490 0.784003765 0.794597379 0.798580013
#> [199] 0.800496429 0.802212294 0.803928159 0.810696494 0.812601592 0.814332458
#> [205] 0.816109094 0.825699105 0.832017757 0.841283357 0.843384650 0.845485943
#> [211] 0.846700494 0.847569963 0.848411813 0.849253664 0.850095515 0.850937366
#> [217] 0.851779216 0.858190762 0.859327414 0.860464067 0.861600719 0.862737372
#> [223] 0.863950565 0.870418822 0.873489408 0.881595506 0.884198926 0.886556676
#> [229] 0.892686437 0.895782054 0.898298137 0.905078816 0.906907677 0.908480820
#> [235] 0.910053963 0.911853796 0.914256935 0.916679219 0.918324101 0.919776591
#> [241] 0.921229081 0.922681571 0.926851815 0.929188669 0.929520183 0.929851696
#> [247] 0.930183209 0.930514722 0.930846236 0.931177749 0.931509262 0.931840775
#> [253] 0.932172289 0.932503802 0.932835315 0.933166828 0.933498342 0.933829855
#> [259] 0.934168546 0.934514805 0.934861064 0.935381570 0.936018848 0.936656125
#> [265] 0.937293403 0.937930681 0.938567958 0.939205236 0.939842514 0.940466145
#> [271] 0.941074998 0.941619396 0.942163794 0.942708193 0.943252591 0.943796989
#> [277] 0.944341388 0.944885786 0.945430184 0.945974583 0.946655934 0.948517069
#> [283] 0.951551533 0.954299892 0.956882950 0.959245478 0.961185694 0.963125909
#> [289] 0.964628540 0.965549515 0.966363299 0.967177082 0.967990866 0.968804650
#> [295] 0.969618433 0.970244179 0.970703924 0.971125165 0.971476756 0.971828346
#> [301] 0.972179937 0.972531527 0.972883117 0.973234708 0.973586298 0.973937888
#> [307] 0.974289479 0.974641069 0.974992660 0.975344250 0.975695840 0.976032570
#> [313] 0.976274003 0.976515435 0.976756868 0.976998300 0.977207513 0.977416496
#> [319] 0.977625480 0.977834464 0.978043447 0.978252431 0.978461415 0.978670398
#> [325] 0.978879382 0.979088366 0.979297349 0.979506333 0.979715317 0.979924300
#> [331] 0.980133284 0.980342268 0.980551251 0.980760235 0.980969219 0.981178202
#> [337] 0.981387186 0.981596170 0.981805153 0.982027026 0.982426534 0.982826042
#> [343] 0.983322906 0.983894857 0.984466807 0.985038757 0.985610708 0.986182658
#> [349] 0.986754609 0.987326559 0.987898509 0.988457586 0.989013811 0.989567104
#> [355] 0.990120398 0.990673691 0.991226984 0.991780278 0.992333571 0.992886864
#> [361] 0.993440158 0.993993451 0.994048518 0.994097618 0.994146717 0.994195816
#> [367] 0.994244916 0.994294015 0.994343115 0.994392214 0.994441313 0.994490413
#> [373] 0.994539512 0.994588611 0.994637711 0.994686810 0.994735910 0.994785009
#> [379] 0.994834108 0.994883208 0.994932307 0.994981407 0.995028186 0.995073551
#> [385] 0.995118917 0.995164282 0.995209648 0.995255013 0.995300379 0.995345744
#> [391] 0.995391110 0.995436475 0.995481841 0.995527206 0.995572572 0.995617937
#> [397] 0.995663303 0.995708668 0.995754034 0.995799399 0.995844765 0.995890130
#> [403] 0.995935495 0.995980861 0.996026226 0.996071592 0.996116957 0.996162323
#> [409] 0.996207688 0.996253054 0.996298419 0.996343785 0.996389150 0.996434516
#> [415] 0.996479881 0.996525247 0.996570612 0.996615978 0.996661343 0.996706708
#> [421] 0.996752074 0.996797439 0.996842805 0.996888170 0.996933536 0.996978901
#> [427] 0.997024267 0.997069632 0.997114998 0.997160363 0.997205729 0.997251094
#> [433] 0.997296460 0.997341825 0.997387191 0.997432556 0.997477922 0.997523287
#> [439] 0.997568652 0.997614018 0.997659383 0.997704749 0.997750114 0.997795480
#> [445] 0.997840845 0.997886211 0.997931576 0.997976942 0.998022307 0.998067673
#> [451] 0.998113038 0.998158404 0.998203769 0.998249135 0.998294500 0.998339866
#> [457] 0.998385231 0.998430596 0.998475962 0.998521327 0.998566693 0.998612058
#> [463] 0.998657424 0.998702789 0.998748155 0.998793520 0.998838886 0.998884251
#> [469] 0.998929617 0.998974982 0.999020348 0.999065713 0.999111079 0.999156444
#> [475] 0.999201810 0.999247175 0.999292540 0.999337906 0.999383271 0.999428637
#> [481] 0.999474002 0.999519368 0.999564733 0.999610099 0.999655464 0.999700830
#> [487] 0.999746195 0.999791561 0.999836926 0.999882292 0.999927657 0.999973023
#> [493] NA
#>
#> $Con_RP
#> [1] NA 6.769358e+00 6.771526e+00 6.773695e+00 6.775865e+00
#> [6] 6.778037e+00 6.780210e+00 6.782384e+00 6.784560e+00 6.786737e+00
#> [11] 6.788916e+00 6.791096e+00 6.793277e+00 6.795460e+00 6.797644e+00
#> [16] 6.799830e+00 6.802017e+00 6.804222e+00 6.806429e+00 6.808638e+00
#> [21] 6.810926e+00 6.813230e+00 6.815536e+00 6.817843e+00 6.820152e+00
#> [26] 6.822463e+00 6.824775e+00 6.827088e+00 6.829404e+00 6.831720e+00
#> [31] 6.834039e+00 6.836359e+00 6.838680e+00 6.841003e+00 6.843328e+00
#> [36] 6.846184e+00 6.849120e+00 6.857547e+00 6.871563e+00 6.885636e+00
#> [41] 6.896991e+00 6.906976e+00 6.916990e+00 6.927034e+00 6.939087e+00
#> [46] 6.953441e+00 6.967855e+00 6.991718e+00 7.022397e+00 7.044013e+00
#> [51] 7.065487e+00 7.086064e+00 7.106650e+00 7.126646e+00 7.146707e+00
#> [56] 7.157092e+00 7.165315e+00 7.173557e+00 7.181818e+00 7.190098e+00
#> [61] 7.227343e+00 7.298861e+00 7.316461e+00 7.334072e+00 7.350666e+00
#> [66] 7.367203e+00 7.381797e+00 7.389595e+00 7.396160e+00 7.402736e+00
#> [71] 7.409324e+00 7.415924e+00 7.422536e+00 7.429799e+00 7.439613e+00
#> [76] 7.451350e+00 7.463124e+00 7.475030e+00 7.529439e+00 7.556452e+00
#> [81] 7.585999e+00 7.632743e+00 7.645605e+00 7.657612e+00 7.669657e+00
#> [86] 7.683309e+00 7.709496e+00 7.736541e+00 7.758269e+00 7.779912e+00
#> [91] 7.811242e+00 7.870500e+00 8.017829e+00 8.033812e+00 8.049858e+00
#> [96] 8.108801e+00 8.163539e+00 8.255032e+00 8.289537e+00 8.347004e+00
#> [101] 8.577866e+00 8.630640e+00 8.668559e+00 8.700629e+00 8.730679e+00
#> [106] 8.777814e+00 8.879826e+00 8.999189e+00 9.114446e+00 9.148437e+00
#> [111] 9.197423e+00 9.275832e+00 9.388277e+00 9.521510e+00 9.574638e+00
#> [116] 9.609421e+00 9.714108e+00 9.821509e+00 9.892863e+00 1.008126e+01
#> [121] 1.042954e+01 1.059416e+01 1.074820e+01 1.080340e+01 1.089589e+01
#> [126] 1.138071e+01 1.144734e+01 1.163782e+01 1.185370e+01 1.190988e+01
#> [131] 1.196921e+01 1.223375e+01 1.230307e+01 1.245595e+01 1.258857e+01
#> [136] 1.268993e+01 1.278578e+01 1.286228e+01 1.295411e+01 1.312620e+01
#> [141] 1.327800e+01 1.335767e+01 1.374590e+01 1.382645e+01 1.390284e+01
#> [146] 1.397548e+01 1.423703e+01 1.439267e+01 1.450172e+01 1.500333e+01
#> [151] 1.541067e+01 1.549282e+01 1.560675e+01 1.609782e+01 1.636629e+01
#> [156] 1.656530e+01 1.676301e+01 1.684515e+01 1.692810e+01 1.701773e+01
#> [161] 1.711395e+01 1.721176e+01 1.732423e+01 1.744130e+01 1.781555e+01
#> [166] 1.803307e+01 1.844081e+01 1.861047e+01 1.870945e+01 1.879535e+01
#> [171] 1.888204e+01 1.929112e+01 1.972373e+01 1.988282e+01 2.043572e+01
#> [176] 2.147014e+01 2.207673e+01 2.238179e+01 2.253730e+01 2.269498e+01
#> [181] 2.333820e+01 2.356113e+01 2.430126e+01 2.462694e+01 2.527223e+01
#> [186] 2.575646e+01 2.614046e+01 2.663712e+01 2.730791e+01 2.775826e+01
#> [191] 2.871336e+01 2.922268e+01 2.976761e+01 3.018363e+01 3.055461e+01
#> [196] 3.114539e+01 3.275171e+01 3.339930e+01 3.372013e+01 3.401266e+01
#> [201] 3.431031e+01 3.553704e+01 3.589831e+01 3.623297e+01 3.658303e+01
#> [206] 3.859582e+01 4.004760e+01 4.238551e+01 4.295419e+01 4.353834e+01
#> [211] 4.388329e+01 4.413360e+01 4.437870e+01 4.462653e+01 4.487715e+01
#> [216] 4.513060e+01 4.538693e+01 4.743898e+01 4.782230e+01 4.821185e+01
#> [221] 4.860781e+01 4.901033e+01 4.944736e+01 5.191561e+01 5.317567e+01
#> [226] 5.681614e+01 5.809347e+01 5.930085e+01 6.268813e+01 6.455017e+01
#> [231] 6.614713e+01 7.087234e+01 7.226467e+01 7.350684e+01 7.479247e+01
#> [236] 7.631963e+01 7.845866e+01 8.073959e+01 8.236562e+01 8.385690e+01
#> [241] 8.540317e+01 8.700754e+01 9.196792e+01 9.500296e+01 9.544982e+01
#> [246] 9.590091e+01 9.635628e+01 9.681599e+01 9.728011e+01 9.774871e+01
#> [251] 9.822184e+01 9.869957e+01 9.918197e+01 9.966911e+01 1.001611e+02
#> [256] 1.006579e+02 1.011597e+02 1.016665e+02 1.021895e+02 1.027299e+02
#> [261] 1.032760e+02 1.041079e+02 1.051448e+02 1.062026e+02 1.072820e+02
#> [266] 1.083834e+02 1.095078e+02 1.106557e+02 1.118279e+02 1.129993e+02
#> [271] 1.141669e+02 1.152315e+02 1.163162e+02 1.174214e+02 1.185479e+02
#> [276] 1.196962e+02 1.208669e+02 1.220608e+02 1.232785e+02 1.245208e+02
#> [281] 1.261112e+02 1.306702e+02 1.388545e+02 1.472050e+02 1.560238e+02
#> [286] 1.650685e+02 1.733198e+02 1.824394e+02 1.901897e+02 1.952741e+02
#> [291] 1.999984e+02 2.049570e+02 2.101677e+02 2.156503e+02 2.214266e+02
#> [296] 2.260830e+02 2.296310e+02 2.329809e+02 2.358528e+02 2.387963e+02
#> [301] 2.418142e+02 2.449094e+02 2.480848e+02 2.513436e+02 2.546893e+02
#> [306] 2.581251e+02 2.616550e+02 2.652827e+02 2.690125e+02 2.728486e+02
#> [311] 2.767957e+02 2.806845e+02 2.835407e+02 2.864556e+02 2.894311e+02
#> [316] 2.924691e+02 2.951537e+02 2.978850e+02 3.006673e+02 3.035021e+02
#> [321] 3.063908e+02 3.093351e+02 3.123365e+02 3.153967e+02 3.185175e+02
#> [326] 3.217006e+02 3.249481e+02 3.282617e+02 3.316436e+02 3.350960e+02
#> [331] 3.386209e+02 3.422209e+02 3.458981e+02 3.496553e+02 3.534950e+02
#> [336] 3.574200e+02 3.614330e+02 3.655373e+02 3.697358e+02 3.743001e+02
#> [341] 3.828093e+02 3.917144e+02 4.033848e+02 4.177104e+02 4.330910e+02
#> [346] 4.496476e+02 4.675203e+02 4.868727e+02 5.078964e+02 5.308176e+02
#> [351] 5.559056e+02 5.828318e+02 6.123403e+02 6.448149e+02 6.809268e+02
#> [356] 7.213235e+02 7.668157e+02 8.184323e+02 8.774993e+02 9.457553e+02
#> [361] 1.025526e+03 1.119992e+03 1.130355e+03 1.139758e+03 1.149318e+03
#> [366] 1.159041e+03 1.168929e+03 1.178988e+03 1.189221e+03 1.199633e+03
#> [371] 1.210229e+03 1.221015e+03 1.231994e+03 1.243172e+03 1.254555e+03
#> [376] 1.266148e+03 1.277958e+03 1.289990e+03 1.302251e+03 1.314747e+03
#> [381] 1.327485e+03 1.340472e+03 1.353085e+03 1.365545e+03 1.378236e+03
#> [386] 1.391166e+03 1.404341e+03 1.417767e+03 1.431453e+03 1.445405e+03
#> [391] 1.459633e+03 1.474143e+03 1.488944e+03 1.504046e+03 1.519457e+03
#> [396] 1.535187e+03 1.551246e+03 1.567645e+03 1.584395e+03 1.601506e+03
#> [401] 1.618990e+03 1.636861e+03 1.655131e+03 1.673813e+03 1.692921e+03
#> [406] 1.712471e+03 1.732478e+03 1.752958e+03 1.773928e+03 1.795405e+03
#> [411] 1.817409e+03 1.839959e+03 1.863076e+03 1.886780e+03 1.911096e+03
#> [416] 1.936047e+03 1.961658e+03 1.987956e+03 2.014968e+03 2.042724e+03
#> [421] 2.071256e+03 2.100596e+03 2.130779e+03 2.161843e+03 2.193825e+03
#> [426] 2.226768e+03 2.260715e+03 2.295714e+03 2.331813e+03 2.369066e+03
#> [431] 2.407528e+03 2.447260e+03 2.488325e+03 2.530791e+03 2.574733e+03
#> [436] 2.620227e+03 2.667358e+03 2.716215e+03 2.766896e+03 2.819504e+03
#> [441] 2.874151e+03 2.930959e+03 2.990057e+03 3.051587e+03 3.115704e+03
#> [446] 3.182572e+03 3.252373e+03 3.325305e+03 3.401583e+03 3.481442e+03
#> [451] 3.565142e+03 3.652964e+03 3.745223e+03 3.842263e+03 3.944466e+03
#> [456] 4.052254e+03 4.166098e+03 4.286524e+03 4.414119e+03 4.549544e+03
#> [461] 4.693541e+03 4.846952e+03 5.010730e+03 5.185963e+03 5.373896e+03
#> [466] 5.575963e+03 5.793819e+03 6.029391e+03 6.284932e+03 6.563092e+03
#> [471] 6.867013e+03 7.200450e+03 7.567920e+03 7.974914e+03 8.428171e+03
#> [476] 8.936055e+03 9.509075e+03 1.016062e+04 1.090802e+04 1.177410e+04
#> [481] 1.278957e+04 1.399674e+04 1.545555e+04 1.725382e+04 1.952565e+04
#> [486] 2.248648e+04 2.650575e+04 3.227455e+04 4.125300e+04 5.715213e+04
#> [491] 9.299162e+04 2.493670e+05 NA
#>
#> $Con_Prob_Est
#> [1] 0.9338179
#>